Autoencoder 的理解远不止于“编码-解码”架构图,掌握其背后的几何与表示本质才能真正提升模型表现:
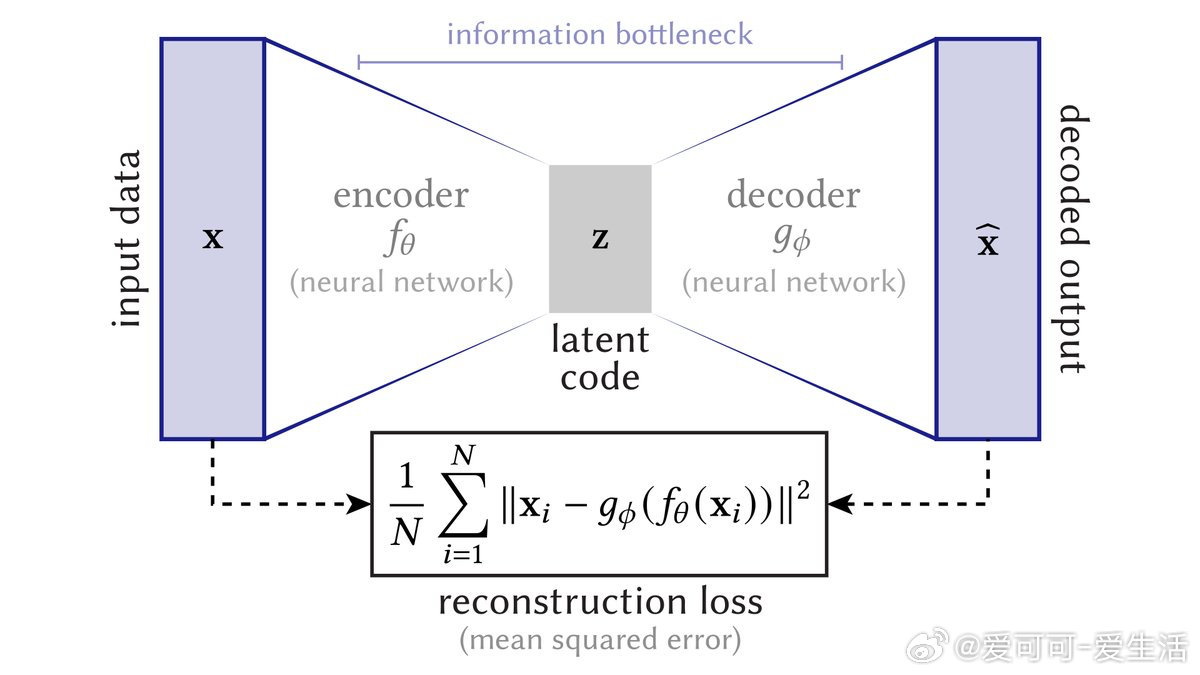
• 常见误区:把 autoencoder 看作仅是网络结构实现,忽视它定义的映射及其几何意义。
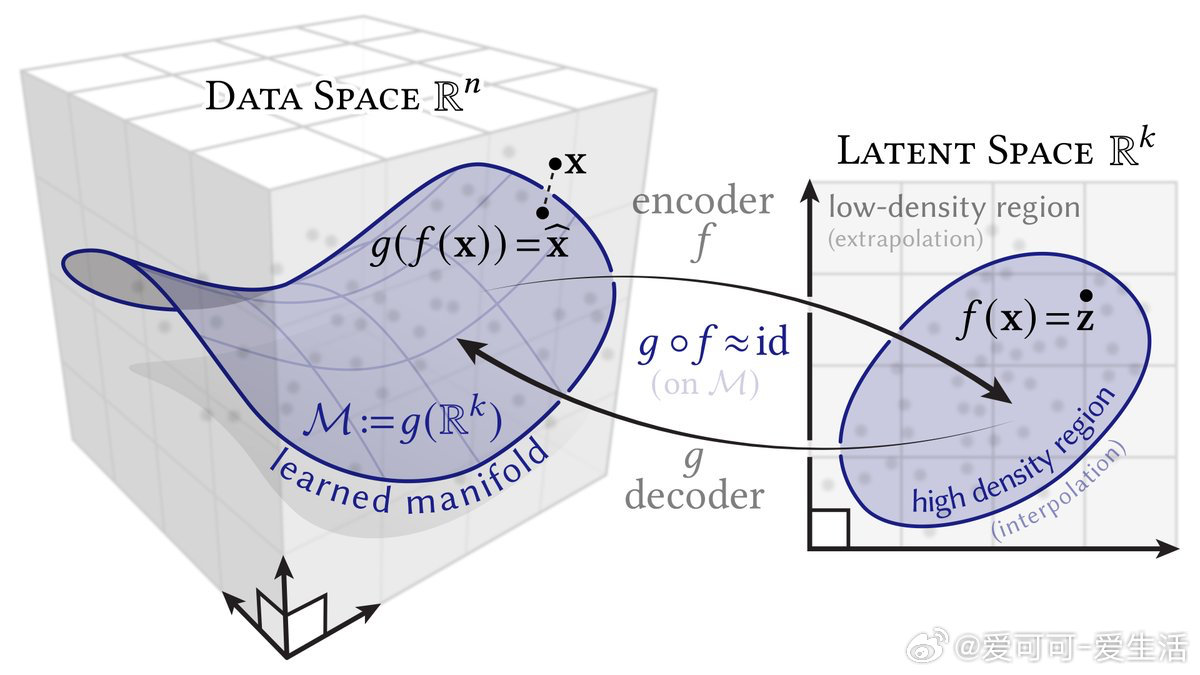
• 核心视角:编码器 f 将高维数据映射到低维潜变量空间,解码器 g 尝试将潜变量映射回数据空间,学习的是潜变量维度 k 的子流形 M。
• 可靠性边界:M 在训练数据密集区域表现良好,缺样区解码器表现为外推,结果不可靠且没有明显边界。
• 潜变量维度即先验:无论真实数据维度如何,解码器产生的流形维度固定为潜空间维度,选择潜变量维数即隐含了对数据结构的假设。
• 重构误差含义:除非损失为零,数据点 x 通常不在 M 上,模型是对数据的近似而非完全拟合,过拟合表现为 M 包含所有训练点。
• 采样难题:普通 autoencoder 无法直接描述潜空间高密度区域,导致随机采样常产生无效样本,变分 autoencoder 等方法为此提供解决方案。
• 直觉提升:理解 autoencoder 不仅是实现,更是学习数据流形的过程,有助于设计更合理的结构和调优策略。
更多图解与深入讨论见🔗 x.com/keenanisalive/status/1964434335911858552
机器学习 深度学习 生成模型 数据流形 自动编码器