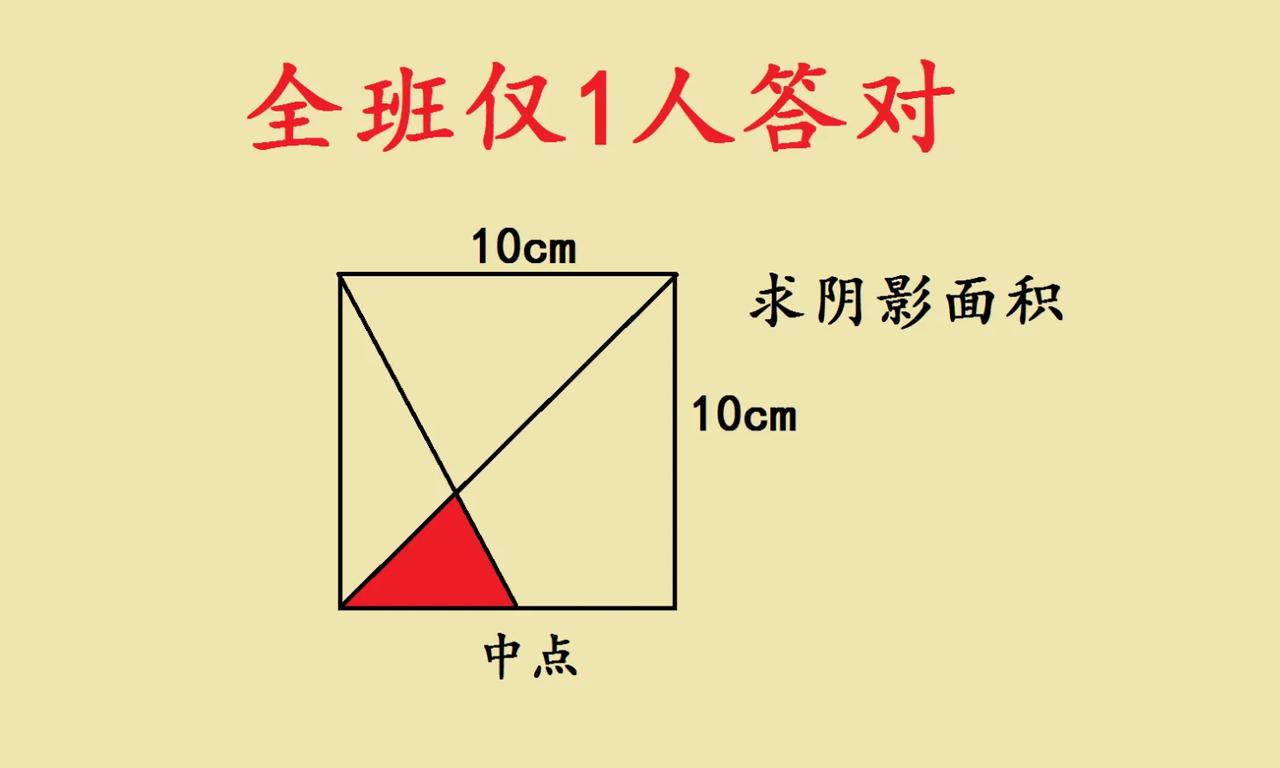
全班仅1人答对的几何题,思维破局点在哪? 看到这道五年级求阴影面积的题,第一眼可能觉得复杂,但换个角度就有突破口。 正方形里的线段、中点,是关键线索。可以联想三角形面积关系,比如等底等高、底边比例与面积比例的关联。把正方形的边、对角线这些元素,和阴影三角形的位置结合,利用图形的对称性、线段中点带来的比例关系,就能找到阴影面积和正方形面积的“隐藏联系”。 很多时候,几何题难在思维固化,总想着直接计算。但只要跳出惯性,观察图形结构,用“转化”的思路——把未知的阴影,转化为已知图形(正方形、大三角形等)的比例部分,答案自然浮现。这道题的巧妙,就藏在对中点的理解、对三角形面积规律的运用里,换个视角看图形,复杂问题也能简单化,你发现这个破局思维了吗?

用户11xxx22
25/3