从非静电力的来源谈磁场运动时的功能关系
雾理悟理
1.问题的提出
当导体棒相对于磁场运动时,若棒克服安培力做功,则棒为发电机(即电源),将机械能转化为电能;若安培力做正功,则棒为电动机,将电能转化为机械能。这就是电磁感应现象中的功能关系。
上述结论在磁场静止的情形下容易理解,没有问题。但当运动磁场带动导体棒运动时,情况则比较复杂,其中的功能关系让人感觉有些混乱。这是怎么回事,又该如何加以解释呢?
2.真题呈现
(2017•江苏)如图所示,两条相距d的平行金属导轨位于同一水平面内,其右端接一阻值为R的电阻。质量为m的金属杆静置在导轨上,其左侧的矩形匀强磁场区域MNPQ的磁感应强度大小为B、方向竖直向下。当该磁场区域以速度v0匀速地向右扫过金属杆后,金属杆的速度变为v. 导轨和金属杆的电阻不计,导轨光滑且足够长,杆在运动过程中始终与导轨垂直且两端与导轨保持良好接触。求:

(1)MN刚扫过金属杆时,杆中感应电流的大小I;
(2)MN刚扫过金属杆时,杆的加速度大小a;
(3)PQ刚要离开金属杆时,感应电流的功率P。

3.第(3)问解析中的疑惑
3.1 参考答案的思路
求解本题的一般思路是:把导体棒视为电源,其等效切割速度为棒相对于磁场的速度,所以棒中的动生电动势大小为:

由于棒相对于磁场的运动方向水平向左,所以棒中感应电流方向向下(俯视),则安培力方向水平向右,如图1所示。

对于试题中的第(3)问,感应电流的功率P应等于感应电流I与感应电动势E的乘积,所以参考答案提供的结果为:
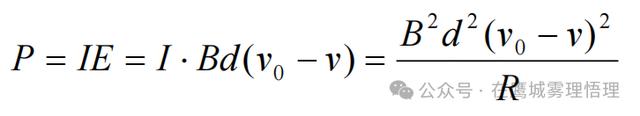
3.2 疑惑之处
从功能关系的角度来看,本情景中,导体棒向右运动,安培力对棒做正功,棒的动能增加,棒应该是电动机。
这样,感应电流的功率应等于回路中的热功率P热与机械功率(即安培力功率)P机之和,所以,当PQ刚要离开金属杆时,应有:

孰对孰错,真相究竟如何呢?
4. 非静电力的来源
为了弄清楚上述功能关系,有必要分析清楚上述情境中的电源中的非静电力来源。
4.1 非静电力是洛伦兹力沿棒方向的分力吗?
必须明确的是,非静电力的方向应与自由电子沿棒定向移动的方向相同。
如图2所示,自由电子定向移动的方向沿棒向上(速率为v定)、随棒运动的速度方向水平向右(速率为v棒)。

可以看到,垂直于棒方向的洛伦兹力的分力f定=ev定B的宏观表现为安培力FA,而平行于棒方向的洛伦兹力分力f棒=ev棒B的方向与自由电子定向移动方向相反,显然也不可能充当非静电力。
4.2 驱动自由电子定向移动的力
究竟是什么力充当了非静电力呢?
为解决这个问题,可以求助于deepseek,解释如下:

原来在观察者看来,当磁场运动时,会在空间产生相对论性电场E. 在本题中,电场E的方向沿棒向下(俯视),且大小E=v0B(由于v0<<c,故洛伦兹因子γ≈1),这样,自由电子受力情况如图3所示.

所以,当磁场运动时,导体棒中的自由电子所受非静电力是相对论性电场所施加的电场力。
5.功能关系
(1)非静电力qv0B做功等于回路产生的电能
从微观上看,非静电力对自由电子做功的功率p=ev0B·v定;而从宏观上看,对应于提供给回路的总电功率P=v0BdI. 从功能关系的角度看,这部分能量等于运动磁场克服磁场力所做的功。
(2)安培力所做的功等于棒增加的动能
通过洛伦兹力的两个分力做功实现将电能转化为棒的动能。
(3)克服静电力F静所做的动
在电源内部,自由电子克服静电力做功使电势能增加,有ΔEP=eE场d=eU. 这部分能量在外电路中通过电阻R转化为焦耳热。
上述能量之间的关系是怎样的呢?
在任意极短时间Δt内,有ev0B=eE场+ev棒B,则dv0B=dE场+dv棒B,即dv0B=U+dv棒B,所以,U=Bd(v0-v棒),式中的U为导体棒两端的电压。
6.结论
综上,当运动的磁场带动导体棒运动时,
(1)能量转化情况是:运动磁场克服磁场力做功将其他形式的能量转化为回路的电能,电能通过电流做功转化为导体棒的动能和回路中的焦耳。
(2)导体棒是电动机模型,安培力所做的功等于棒增加的动能。
(3)感应电流的功率等于回路的热功率与安培力功率之和。
7.反思
在相对论中,电磁场具有统一性,电场与磁场随参考系的变换而相互转化。在命制有关运动磁场的电磁感应问题时,要注意高中生的接受能力和参考答案的科学性,尽量避免使学生陷入混淆或者不必要的疑难之中。
